Una de las herramientas más interesantes con la que podemos contar en el análisis de activos financieros es la relativa a los tipos de distribución de probabilidad. ¿Por qué? Porque permite plantear escenarios probabilísticos respecto de los activos financieros y su comportamiento futuro, a fin de tomar decisiones racionales en lo que respecta a la gestión de esos activos en las carteras de inversión.
De la mano de Andrés Muñoz, en este artículo vamos a ver dos modelos de distribución de probabilidad que nos pueden ayudar enormemente:
Distribución de probabilidad continua de variable aleatoria discreta
Una variable aleatoria es aquella cuyo comportamiento futuro es impredecible, por depender de factores que no podemos modelizar de manera determinista. Si esta variable es discreta solo podrá tomar una serie de valores, acotados en un rango concreto de posibilidades. Por ejemplo, el número de empresas cotizadas en un índice bursátil no puede tomar valores decimales o ratios, solamente valores discretos (veinte, cien, quinientos, etc.).
Una función de distribución discreta de la probabilidad supone que se le asignan las mismas probabilidades, de forma lineal, a todos los posibles eventos. Por ejemplo, si tiramos un dado de 6 caras, asumiendo un modelo de este tipo, diremos que cada cara del dado tiene un 1/6 de probabilidades de salir, esto es, una sexta parte.
Veamos un ejemplo con activos financieros. Pensemos en un bono de deuda privada que se emite por una compañía de nueva creación que desea financiar parte de sus inversiones a largo plazo. Ese bono pagará un cupón del 2% anual para los inversores. Pero si el EBITDA supera los 10 millones en su primer año de actividad, pagará un 4 % en vez de un 2%. Alternativamente, si el EBITDA supera los 20 millones en su primer año, pagará un 6%. Finalmente, si el EBITDA superase los 30 millones pagaría un 8%. Según cada evento, podemos ver en el cuadro de abajo el cupón que correspondería al inversionista.
| Evento | Cupón anual |
| EBITDA < 10 Millones € | 2% |
| EBITDA entre 10 y 20 Millones € | 4% |
| EBITDA entre 20 y 30 Millones € | 6% |
| EBITDA > 30 Millones € | 8% |
Modelo simple continuo
Si como asesores financieros queremos plantear un escenario de probabilidades para un inversor, y dado que no tenemos datos históricos ni ninguna otra variable con la cual especular sobre qué EBITDA podrá conseguir la compañía, podríamos utilizar un modelo de probabilidades simple continuo, en el cual, habiendo 4 posibles escenarios, es decir 2%, 4%, 6% y 8%, otorguemos un 25% de probabilidades a cada escenario. Es decir, 1/4 de probabilidad para cada evento. Por lo que podríamos dar un 25% de probabilidades a cobrar el 2%, un 25% de cobrar el 4%, un 25% de cobrar el 6% y un 25% de probabilidades del 8%.
| Evento | Cupón anual | Probabilidad |
| EBITDA < 10 Millones € | 2% | 25% |
| EBITDA entre 10 y 20 Millones € | 4% | 25% |
| EBITDA entre 20 y 30 Millones € | 6% | 25% |
| EBITDA > 30 Millones € | 8% | 25% |
¿Y si por ejemplo nos preguntan que cuántas probabilidades hay de obtener más de un 4%? Si sumamos las probabilidades del 6% y del 8% (lo cual son escenarios que cumplen con lo que se pregunta) el resultado sería que existen un 50% de probabilidades de cobrar más del 4%.
Y si tenemos un histórico…
Avanzando sobre esta idea, imaginemos ahora otro ejemplo en el cual tuviésemos un bono similar al anterior, pero de una compañía que lleva diez años en el mercado, y por tanto hay un histórico de su actividad que podemos analizar. Si estudiamos ese histórico de EBITDA a lo largo de esos diez años, y resulta que hay 4 años en los que ha conseguido un EBITDA por debajo de 10 millones de euros, 4 años en los que ha conseguido un EBITDA entre 10 y 20 millones, un año en el cual consiguió un EBITDA entre 20 y 30 millones, y 1 año en el que superó los 30 millones.
Nuestro escenario de probabilidades podría ser el siguiente: otorgamos un 40% de probabilidades a obtener un 2%, un 40% de probabilidades a obtener un 4%, un 10% de probabilidades a lograr un 6% y un 10% de probabilidades de conseguir un 8%. Una forma de verlo sería decir que existen un 80% de probabilidades de conseguir una rentabilidad máxima del 4%.
| Evento | Cupón anual | Probabilidad |
| EBITDA < 10 Millones € | 2% | 40% |
| EBITDA entre 10 y 20 Millones € | 4% | 40% |
| EBITDA entre 20 y 30 Millones € | 6% | 10% |
| EBITDA > 30 Millones € | 8% | 10% |
De esta forma podemos aseverar que con un 80% de probabilidades la rentabilidad máxima esperada será de 4% y la mínima será del 2%, a fin de asesorar a un inversionista y comparar con otras inversiones alternativas. En suma, este modelo de plantear escenarios de probabilidad para la toma decisiones puede resultar muy sencillo pero también muy efectivo.
Distribución de probabilidad normal
Es posiblemente el modelo más conocido, y seguramente el más utilizado en las finanzas modernas. Se basa en usar la distribución normal de probabilidad, que tiene forma de “campana” y se suele denominar “campana de Gauss”, o bien “distribución de Laplace”, o directamente distribución normal estadística.
El origen de este modelo lo encontramos en el trabajo del matemático francés Abraham de Moivre en 1.733 como aproximación a la distribución binomial (una variante de la distribución continua de variables aleatorias que vimos antes) cuando el número de resultados es muy elevado.
Lo cierto es que en la práctica y en muy diversos campos (física, observación natural, genética, medicina, sociología, economía, etc.) se ha comprobado empíricamente que este modelo funciona bien cuando trabajamos con grandes números.
Las dos variables sobre las que pibota el modelo son la media y la desviación típica. Recordemos que la media es el resultado de sumar todas las observaciones y dividirlo por el número de observaciones, por lo cual nos muestra el valor medio de la serie. Mientras la desviación típica es la raíz cuadrada (para evitar el efecto del cuadrado que ahora veremos) del quebrado que tiene por numerador el sumatorio al cuadrado de la diferencia entre cada observación de la serie respecto de la media (el cuadrado se usa para evitar números negativos), y por denominador el número de observaciones. Es decir, nos muestra la dispersión típica entre las observaciones y la media).
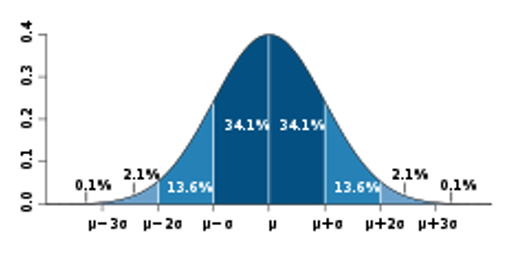
El modelo se basa en que las distribuciones de grandes series estadísticas suelen agruparse en torno a la media de la siguiente forma:
Con un 34,1% de probabilidades las observaciones tienden a situarse en la media más la desviación típica; y con un 34,1% de probabilidades las observaciones tienden a situarse en la media menos la desviación típica.
Con un 47,7% de probabilidades las observaciones tienden a situarse en la media más dos veces la desviación típica; y con un 47,7% de probabilidades las observaciones tienden a situarse en la media menos dos veces la desviación típica.
Con un 49,8% de probabilidades las observaciones tienden a situarse en la media más tres veces la desviación típica; y con un 49,8% de probabilidades las observaciones tienden a situarse en la media menos tres veces la desviación típica.
Algunos resultados importantes de los seis puntos previos es lo siguiente:
- Solo un 0,2% de las observaciones tienden a estar por encima de la media más tres veces la desviación, o por debajo de la media menos tres veces la desviación.
- Un 50% de las observaciones tienden a estar por encima de la media (49,8% de la media más tres veces la desviación, y más el 0,2% residual de la cola por arriba) y el otro 50% de las observaciones tienden a estar por debajo de la media (49,8% de la media menos tres veces la desviación, y más el 0,2% residual de la cola por abajo).
Veamos un ejemplo de escenarios de probabilidad en asesoramiento financiero utilizando este modelo. Pensemos en la cotización de las acciones de una empresa muy importante, de gran capitalización y que cotiza en el Dow Jones, por lo cual tiene cada día decenas de miles de órdenes de compra y venta. En una coyuntura económica estándar, asumimos que su cotización puede variar siguiendo una distribución normal. Cogemos el valor de la acción en los últimos 500 días de cotización, y obtenemos como resultado una cotización media de 100 $.
Seguimos…
Calculamos la desviación típica, y obtenemos 30 $. Si tenemos que presentar un escenario de probabilidades respecto de qué sucederá con la acción en su cotización durante el próximo año, en base a estos datos, el escenario sería el siguiente:
| Grado de probabilidad | Valoración |
| 34,1 % | Entre 100 $ y 130 $ |
| 13,6 % | Entre 130 $ y 160 $ |
| 2,1 % | Entre 160 $ y 190 $ |
| 0,2 % | Más de 190 $ |
| 34,1 % | Entre 100 $ y 70 $ |
| 13,6 % | Entre 70 $ y 40 $ |
| 2,1 % | Entre 40 $ y 10 $ |
| 0,2 % | Menos de 10 $ |
De esta forma por tanto podremos asesorar a un inversionista, haciendo aseveraciones como que será muy poco probable que llegue a tener una revalorización en torno al 200% con esta acción (pasar de 100 $ a 200 $ estaría por debajo del 0,2 % de probabilidad) pero igualmente es muy poco probable llegar a perder más del 90% del valor invertido (que cotice por debajo de 10 $ tiene una probabilidad también por debajo del 0,2 %. Lo más probable es que el valor de cotización se mueva entre 70 $ y 130 $, a lo cual podemos otorgar unas probabilidades del 68,2 %, y esto nos permitiría comparar con otra inversión similar en la cual podamos asumir para ese mismo rango de probabilidad una horquilla diferente.
En definitiva, el planteamiento de escenarios de probabilidad es sumamente importante en el análisis financiero, y estos sencillos modelos pueden ser de gran utilidad para analistas y asesores.


































